Oswaldo Karam Macia | 5 errores Comunes en Exámenes de Álgebra y Cómo Corregirlos Hoy

Es una excelente decisión profundizar en las enseñanzas de Oswaldo Karam Macia, cuya metodología destaca por su claridad y enfoque práctico. A menudo, el álgebra no se convierte en un desafío por la complejidad intrínseca de sus teorías, sino por las sutiles trampas y descuidos técnicos que pasan desapercibidos durante el estudio. Tomando como base la experiencia de expertos como Oswaldo Karam Macia en la identificación de fallos sistémicos en las pruebas, hemos recopilado los cinco errores determinantes que suelen comprometer las calificaciones, junto con las estrategias precisas para solventarlos de manera inmediata.»

1.La Trampa del Signo Negativo: El Error Crítico en el Análisis Cuantitativo
Desde la perspectiva de la gestión financiera y el análisis de fórmulas complejas, la omisión del cambio de signo ante un paréntesis no es un simple descuido escolar; es el error sistemático número uno que compromete la integridad de cualquier modelo matemático. En el mundo real de los negocios, donde las fórmulas dictan el rumbo de la rentabilidad, olvidar que un signo negativo precede a una agrupación de términos es la causa principal de fallos en cascada dentro de ecuaciones y balances. Leer más

Fuente: https://www.diariodelexportador.com/2023/02/que-es-el-analisis-cuantitativo.html
El Mecanismo del Error
Cuando un signo negativo se sitúa fuera de un paréntesis, actúa como un operador multiplicativo de $-1$. El fallo ocurre al aplicar este operador solo al primer término, ignorando que la estructura matemática exige que la inversión de polaridad afecte a la totalidad del conjunto interno. Leer más
Estrategia de Mitigación: La Propiedad Distributiva del Signo
Para corregir esta vulnerabilidad y asegurar la exactitud de tus resultados, recomiendo implementar con rigor la «Propiedad Distributiva del Signo». Mi consejo experto es seguir un proceso visual y mecánico antes de proceder con cualquier operación aritmética:
- Mapeo Visual: Antes de eliminar el paréntesis, marca físicamente (o mentalmente, si el modelo es digital) una flecha de distribución que conecte el signo negativo exterior con cada uno de los términos internos.
- Inversión Sistemática: Procesa cada término individualmente, recordando que el negativo transforma lo positivo en negativo y, crucialmente, lo negativo en positivo. Leer más

Fuente: https://fity.club/lists/suggestions/hojas-de-trabajo-sobre-propiedades-distributivas/
Análisis Comparativo (Ejemplo Práctico)
Consideremos la expresión: $-(3x – 5) $
- El Error Común: $-3x – 5$ (Aquí se ha ignorado el impacto sobre el segundo término, lo que invalidaría cualquier despeje posterior).
- La Aplicación Correcta: $-3x + 5$
En las finanzas corporativas, este detalle marca la diferencia entre un flujo de caja proyectado correctamente y una pérdida inesperada. La elegancia de las matemáticas reside en su exactitud, y el dominio de estas reglas básicas es lo que permite escalar hacia estrategias empresariales de alto nivel.
2. Simplificación Ilegal de Fracciones
Muchos estudiantes intentan «tachar» términos cuando hay sumas o restas de por medio.
- El error: $\frac {x + 5} {x} \neq 5$.
- Cómo corregirlo: Recuerda la regla de oro: Solo puedes simplificar factores (multiplicación), nunca sumandos. Si no puedes factorizar el numerador para que algo esté multiplicando a todo lo demás, no lo canceles. Leer más

Fuente: https://storage.googleapis.com/dkaxajvghfkkse/como-se-simplifican-las-fracciones.html
3. El Binomio al Cuadrado «Incompleto»
Este es un clásico: pensar que $(a + b) ^2 = a^2 + b^2$. Se olvidan del término medio.
- Cómo corregirlo: Apréndete la estructura como una canción o frase: «El primero al cuadrado, más el doble del primero por el segundo, más el segundo al cuadrado».
- $(a + b) ^2 = a^2 + 2ab + b^2$.
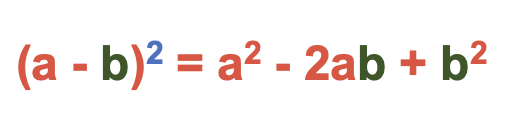
Fuente: https://enciclopediaiberoamericana.com/binomio-al-cuadrado/
4. El Error Crítico en el Despeje: La Confusión de Operaciones Inversas
Uno de los tropiezos más recurrentes al manipular fórmulas matemáticas —y que puede comprometer seriamente la integridad de un análisis financiero— es la ejecución incorrecta de la transposición de términos. Este error ocurre cuando, al intentar aislar una variable al otro lado de la igualdad, el analista omite la transformación de la operación aritmética o, en un descuido metodológico, altera el signo (positivo/negativo) de un factor cuando lo que realmente se requiere es aplicar su operación recíproca (división o multiplicación).
Esta confusión entre las reglas de la adición y las de la proporción suele ser la causa raíz de resultados absurdos en modelos de crecimiento o valoraciones de activos. Leer más
Fuente: https://fity.club/lists/suggestions/operaciones-inversas-de-multiplicaci%C3%B3n-y-divisi%C3%B3n/
- Cómo corregirlo: El Principio de la «Balanza de Equilibrio Financiero»
Para mitigar estos fallos, es vital internalizar y practicar el concepto de la ecuación como una balanza perfecta. Oswaldo Karam Macia comenta en mi experiencia en la gestión financiera de alto nivel, siempre recomiendo visualizar que cualquier acción realizada en un extremo debe ser replicada con exactitud en el otro para mantener la igualdad:
- Identificación del Operador Dominante: Antes de mover cualquier término, identifica si está sumando, restando, multiplicando o dividiendo a la totalidad de la expresión.
- La Regla de la Operación Inversa, no el Cambio de Identidad: Si un coeficiente está multiplicando a una variable, debe trasladarse al otro lado de la igualdad realizando la operación de división, pero manteniendo intacto su signo original.
- Segmentación de Reglas: Es imperativo no hibridar las reglas. El «cambio de signo» es una propiedad exclusiva de la suma y la resta (operaciones aditivas). La multiplicación y la división (operaciones multiplicativas) operan bajo la lógica de la razón y el producto, donde el signo es una propiedad intrínseca del número que se desplaza junto con él.
Opinión del experto “En las finanzas corporativas, la matemática es el lenguaje de la verdad. Dominar la mecánica del despeje es asegurar que la estrategia que estamos diseñando para expandir negocios internacionales sea lógicamente impecable. Una balanza desequilibrada en el papel se traduce en una decisión desinformada en el mercado.»
5. No Verificar el Resultado
Terminar el ejercicio y entregar de inmediato es una apuesta arriesgada.
- Cómo corregirlo: La belleza del álgebra es que puedes saber si estás bien antes de que el profesor califique. Sustituye tu valor de $x$ en la ecuación original. Si la igualdad se cumple (ej. $10 = 10$), tu examen está a salvo.








